Home  ›  How to Read a Root Locus Plot

How to Read a Root Locus Plot

Written By Tuesday, March 1, 2022 Add Comment Edit

Introduction: Root Locus Controller Blueprint

In this tutorial, we will introduce the root locus, bear witness how to create information technology using MATLAB, and demonstrate how to blueprint feedback controllers that satisfy certain performance criteria through the use of the root locus.

Key MATLAB commands used in this tutorial are: feedback , rlocus , footstep , controlSystemDesigner

Run Live Script Version in MATLAB Online

Contents

  • Closed-Loop Poles
  • Plotting the Root Locus of a Transfer Office
  • Choosing a Value of K from the Root Locus
  • Closed-Loop Response
  • Using Command Organization Designer for Root Locus Pattern

Closed-Loop Poles

The root locus of an (open-loop) transfer function $H(s)$ is a plot of the locations (locus) of all possible airtight-loop poles with some parameter, frequently a proportional gain $K$, varied between 0 and $\infty$. The figure below shows a unity-feedback compages, only the procedure is identical for whatsoever open up-loop transfer function $H(s)$, fifty-fifty if some elements of the open-loop transfer role are in the feedback path.

The airtight-loop transfer function in this case is:

(i) $$ \frac{Y(s)}{R(s)} = \frac{KH(s)}{1 + KH(s)} $$

and thus the poles of the closed-loop system are values of $s$ such that $1 + KH(s) = 0$.

If we write $H(s) = b(s)/a(s)$, and then this equation tin be rewritten as:

(two) $$ \Rightarrow\ a(s) + Kb(s) = 0 $$

(3) $$ \Rightarrow\ \frac{a(s)}{K} + b(s) = 0 $$

Let $n$ be the order of $a(s)$ and $m$ exist the order of $b(s)$ (the gild of the polynomial corresponds to the highest power of $s$).

We will consider all positive values of $K$. In the limit equally $K \rightarrow 0$, the poles of the closed-loop system are solutions of $a(s) = 0$ (poles of $H(s)$). In the limit as $K \rightarrow \infty$, the poles of the closed-loop system are solutions of $b(s) = 0$ (zeros of $H(s)$).

No matter our choice of $K$, the closed-loop system has $n$ poles, where $n$ is the number of poles of the open-loop transfer function $H(s)$. The root locus then has $n$ branches, each branch starts at a pole of $H(s)$ and approaches a nada of $H(s)$. If $H(s)$ has more poles than zeros (as is frequently the case), $m < n$ and we say that $H(s)$ has zeros at infinity. In this case, the limit of $H(s)$ as $s \rightarrow \infty$ is cipher. The number of zeros at infinity is $n-m$, the number of open-loop poles minus the number of open-loop zeros, and is the number of branches of the root locus that go to "infinity" (asymptotes).

Since the root locus consists of the locations of all possible airtight-loop poles, the root locus helps us cull the value of the gain $K$ to achieve the type of operation we want. If any of the selected poles are on the correct-one-half circuitous plane, the airtight-loop organisation will be unstable. The poles that are closest to the imaginary axis have the greatest influence on the airtight-loop response, so fifty-fifty if a system has iii or four poles, it may still conduct like to a second- or a outset-order organization, depending on the location(southward) of the dominant pole(s).

Plotting the Root Locus of a Transfer Function

Consider an open up-loop system which has a transfer function of

(4) $$ H(s) = \frac{Y(s)}{U(s)} = \frac{s + 7}{s(s + 5)(s + 15)(s + 20)} $$

How practice we design a feedback controller for the system using the root-locus method? Permit'southward assume our design criteria are 5% overshoot and 1 second ascension time. Create an yard-file titled rl.m. Within this file, create the transfer function model and utilize the rlocus command as follows: 

s = tf('s'); sys = (s + 7)/(s*(s + 5)*(s + 15)*(due south + twenty)); rlocus(sys) axis([-22 3 -15 15])

Choosing a Value of Thousand from the Root Locus

The plot above shows all possible airtight-loop pole locations for a pure proportional controller. In this instance, non all of these closed-loop pole locations indicate satisfaction of our design criteria. To determine what part of the locus is acceptable, we tin utilize the control sgrid(zeta,wn) to plot lines of constant damping ratio and natural frequency. Its 2 arguments are the damping ratio ($\zeta$) and natural frequency ($\omega_n$) [these may be vectors if you want to look at a range of adequate values]. In our problem, we need an overshoot less than five% (which means a damping ratio $\zeta$ of greater than 0.7) and a rise time of 1 second (which means a natural frequency $\omega_n$ greater than 1.8). Enter the post-obit in the MATLAB command window: 

zeta = 0.7; wn = 1.eight; sgrid(zeta,wn)

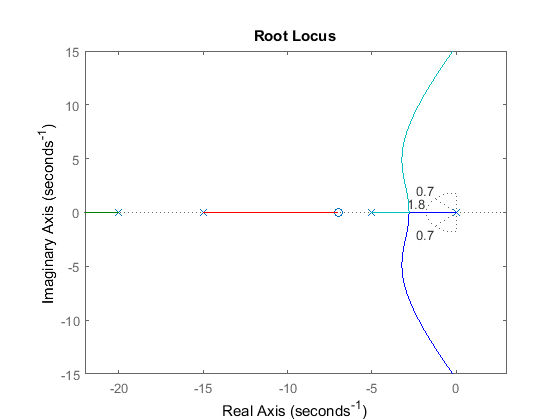
On the plot above, the two dotted lines at about a 45-degree angle indicate pole locations with $\zeta$ = 0.7; in between these lines, the poles volition take $\zeta$ > 0.7 and outside of these lines $\zeta$ < 0.seven. The semicircle indicates pole locations with a natural frequency $\omega_n$ = 1.8; inside of the circle, $\omega_n$ < 1.8 and outside of the circumvolve $\omega_n$ > 1.8.

Going dorsum to our problem, to make the overshoot less than 5%, the poles have to be in between the ii angled dotted lines, and to make the rise time shorter than ane 2nd, the poles have to exist outside of the dotted semicircle. So now we know what part of the root locus, which possible closed-loop pole locations, satify the given requirements. All the poles in this location are in the left-half plane, and then the closed-loop system volition be stable.

From the plot above we come across that in that location is function of the root locus inside the desired region. Therefore, in this case, we need simply a proportional controller to motility the poles to the desired region. You can use the rlocfind command in MATLAB to cull the desired poles on the locus:

[k,poles] = rlocfind(sys)

Click on the plot the point where you desire the airtight-loop pole to be. You may want to select the points indicated in the plot below to satisfy the design criteria.

Annotation that since the root locus may accept more than than ane branch, when you select a pole, you besides identify where other closed-loop poles are too, all for the same respective value of $K$. Remember that these poles will affect the response too. From the plot above, we see that of the four poles selected (indicated by "+" signs), the two closest to the imaginary axis are in our desired region. Since these poles tend to dominate the response, we have some confidence that are desired requirements volition be met for a proportional controller with this value of $K$.

Closed-Loop Response

In order to verify the step response, you demand to know the closed-loop transfer part. You could compute this using the rules of block diagram reduction, or let MATLAB do information technology for you (there is no demand to enter a value for K if the rlocfind command was used): 

Chiliad = 350; sys_cl = feedback(K*sys,i)        
sys_cl =                  350 s + 2450   --------------------------------------   due south^4 + 40 s^iii + 475 due south^2 + 1850 s + 2450   Continuous-time transfer office.

The two arguments to the part feedback are the transfer function in the forward path and the transfer function in the feedback path of the open-loop organization. In this case, our system is unity feedback.

If y'all have a non-unity feedback situation, wait at the aid file for the MATLAB function feedback, which demonstrates how to find the closed-loop transfer function with a gain in the feedback path.

Checking the step response of the closed-loop system with the chosen value of $K$: 

stride(sys_cl)

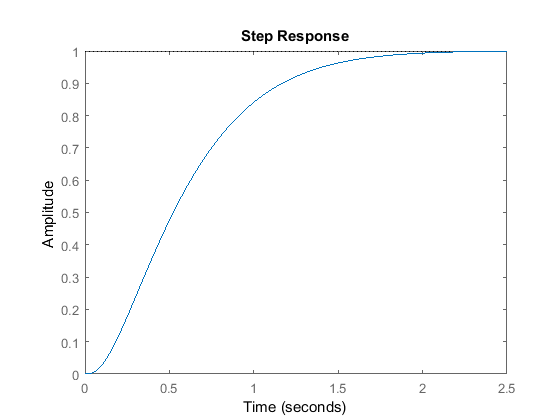
Equally we expected, this response has an overshoot less than 5% and a ascension time less than 1 second.

Using Control System Designer for Root Locus Design

Another way to complete what was washed above is to use the interactive Control Organisation Designer tool within MATLAB. Using the same model as in a higher place, we starting time define the plant, $H(s)$. 

south = tf('south'); institute = (s + seven)/(southward*(southward + v)*(southward + xv)*(s + xx));

The controlSystemDesigner function can exist used for assay and blueprint. In this instance, nosotros will focus on using the root locus as the design method to ameliorate the step response of the closed-loop arrangement. To brainstorm, type the following into the MATLAB command window:

controlSystemDesigner(establish)

The following window should appear. You lot can also launch the GUI by going to the APPS tab and clicking on the app icon nether Command System Pattern and Analysis. Here you can see the root locus plot, forth with open up-loop Bode plot, and the closed-loop step response plot for the given establish in unity feedback with a default controller of $K = 1$.

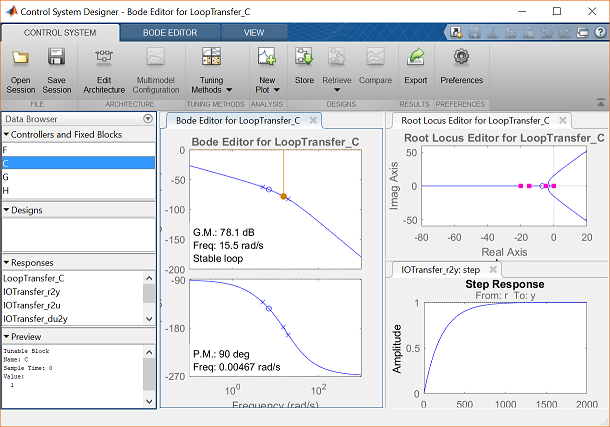
The adjacent stride is to add the design requirements to the Root Locus plot. This is washed directly on the plot by correct-clicking and selecting Design Requirements, New. Pattern requirements tin exist prepare for the Settling Time, the Percent Overshoot, the Damping Ratio, the Natural Frequency, or a Region Constraint.

Hither, nosotros will gear up the blueprint requirements for the damping ratio and the natural frequency as was done previously with the sgrid command. Retrieve that the purlieus of our requirements call for $\zeta$ = 0.7 and $\omega_n$ = ane.viii. Set these within the design requirements. On the plot, any area which is still white is an acceptable region for the closed-loop poles.

Zoom into the Root Locus by correct-clicking on an axis and selecting Properties followed by the label Limits. Change the real-axis limits to -25 to 5 and the imaginary axis limits to -2.v to 2.5.

Also, nosotros tin can see the current values of some key parameters in the response. On the Step response plot, right-click on the plot and go to Characteristics and select Acme Response. Repeat for the feature Rise Time. At that place should at present be two big dots on the screen indicating the values of these parameters. Click each of these dots to bring up a box with information.

Both plots should appear equally shown here, once the Bode plot is airtight:

As the characteristics bear witness on the Footstep response, the overshoot is acceptable, merely the ascent time is much likewise large. The pinkish boxes on the root locus testify the corresponding closed-loop pole locations for the currently chosen control gain $K$.

To gear up this, we need to cull a new value for the gain $K$. Similar to how nosotros employed the rlocfind command, the proceeds of the controller tin exist changed directly on the root locus plot. Click and drag the pink box closest to the imaginary centrality (at the origin) to the acceptable region of our root locus plot as shown below.

In the Preview box of the window, information technology can exist seen that the loop gain has been changed to 360. Inspecting the closed-loop stride response plot, both of our requirements are now met.

All contents licensed under a Creative Commons Attribution-ShareAlike four.0 International License.

holmesthail1981.blogspot.com

Source: https://ctms.engin.umich.edu/CTMS/index.php?example=Introduction§ion=ControlRootLocus

0 Response to "How to Read a Root Locus Plot"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel